Like numbers, definition of
square root can be extended for matrices. A matrix
B is said to be a square root of
A if
B2=A. For example square roots of the matrix
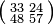
are

,

and their additive inverses.
There are a number of methods for calculating square roots of matrices. One of the frequently used method is diagonalization method. An
n×n matrix
A is diagonalizable if there is a matrix
V and a diagonal matrix
D such that
A = VD-1V . This happens if and only if
A has
n eigenvectors which constitute a basis for
Cn. In this case,
V can be chosen to be the matrix with the
n eigenvectors as columns, and a square root of
A is
VSV-1, where
S is any square root of
D. Indeed,
(VD1/2V-1)2 = VD1/2(V-1V)D1/2V-1 = VDV-1 = A .
As in the example, the matrix

can be diagonalized as

, where

and

.
D has principal square root

, giving the square root

.
Ref: Wikipedia


