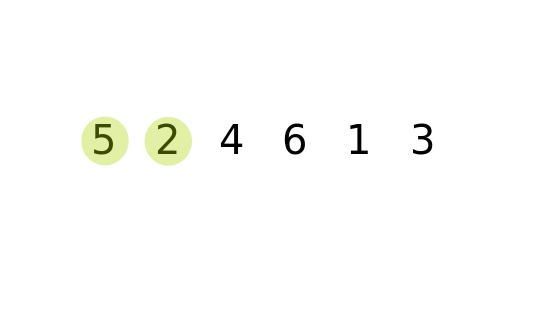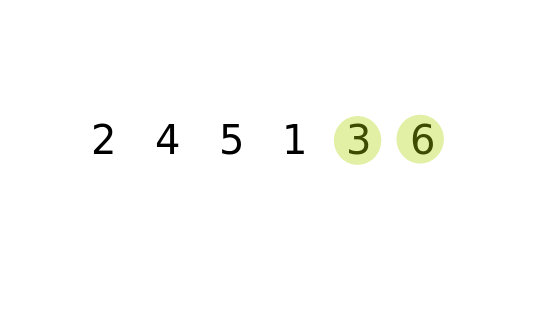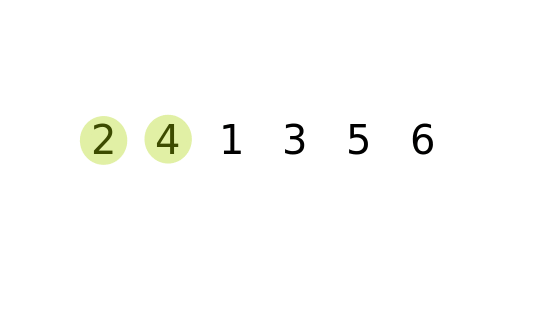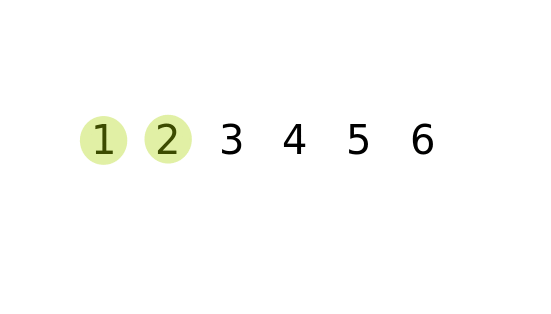Messages

1

Science and Information / এলগরিদমের খুঁটিনাটি ৪র্থ পর্ব ( Mergesort Algorithm )

« on: October 14, 2017, 10:01:09 PM »

    আজ যে এলগরিদমটা নিয়ে আলোচনা করব , সেটার নাম মার্জ সর্ট এলগরিদম । শুরুতেই কিছু কথা বলে নেয়া যাক ~ একটা সমস্যা সমাধানের জন্য কয়েকটা এলগরিদম থাকতে পারে । এই যেমন সর্টিং এর জন্য
Bubble Sort , Insertion Sort  , Selection Sort , Quicksort , Mergesort , Heapsort  এলগরিদম রয়েছে ।
প্রশ্ন হচ্ছে এতগুলো এলগরিদমের মধ্যথেকে কোনটা বেছে নিব ? এলগরিদমের দুইটা বৈশিষ্টের উপর ভিত্তি করে আমরা বেস্ট এলগরিদম বেছে নিব ।
   Correctness
   Efficiency 
কিভাবে একটা এলগরিদমের কারেক্টনেস এবং ইফিসিয়েন্সি বের করে সেটা নিয়ে আরেক দিন লেখব । সর্টিং এলগরিদমের মধ্যে সবচেয়ে কার্যকর এলরিদম হচ্ছে Mergesort এলগরিদম । চলুন Mergesort এলগরিদমের সাথে পরিচয় পর্ব শেষ করা যাক । Mergesort এলগরিদমকে  Divide and Conquer  এলগরিদমও বলাহয়ে থাকে ।
১৯৪৫ সালে John von Neumann নামের হাঙ্গেরিয়ান - আমেরিকান গণিতবিদ Mergesort এলগরিদম আবিষ্কার করেন । চলুন শুরু করা যাক 
ধরুন আপনার কাছে আনসর্টেট একটা array আছে , নিচের চিত্রে খেয়াল করুন


আমরা গত পর্বে দেখেছিলাম কিভাবে বাবল সর্ট এলগরিদম ফলো করে খুব সহজেই একটা আনসর্টেড অ্যারে সর্ট করা যায় ।  Mergesort এলগরিদম পুরোপুরি ভিন্নভাবে কম সময়ে এই কাজটা সম্পন্ন করে ! এজন্য Divide and Conquer নিয়ম ফলো করতে হয় ।
প্রথমেই আনসর্টেড অ্যারেকে দুই ভাগে ভাগ করে নিতে হবে , নিচের চিত্রে খেয়াল করুন 

 
এভাবে যতক্ষণ ভাগ (ডিভাইড) করা যায় , মূলকথা হচ্ছে আমরা মেইন লিস্ট থেকে সাবলিস্ট তৈরি করে বড় সমস্যাটাকে ছোট ছোট অংশে ভাগ করে দিচ্ছি । ছোট অংশগুলোকে যখন সমাধান করে  মার্জ করব , তখন আমরা বড় সমস্যাটার সমাধান পেয়ে যাব । চলুন উপরের দুইটা সাবলিস্টকে আবারো ডিভাইড করা যাক

এভাবে আমরা সাবলিস্ট তিরী করতে থাকব যতক্ষণ পর্যন্ত আমাদের সাবলিস্ট বানানোর অপশন থাকবে , নিচের চিত্রে খেয়াল করুন –                             
 
       
এবারে আর কোন সাবলিস্ট তৈরী করা সম্ভব নয় , এবারে ভাগকরা সর্বশেষ দুইটা এলিমেন্টের মধ্যে কম্পেয়ারিং শুরু করব । যেহেতু ২ < ৪৫  , সেহেতু এখানে কোন পরিবর্তন হবে না । ২ আর ৪৫ কে আগের অবস্থায় রেখে দিব । আবার ৫ < ৫১ তাই এখানেও কোন পরিবর্তন হবে না , তাই তাদের কেও আগের অবস্থায় রেখে দিব  ।
এবারে ডান পাশের ১ এবং ৩৫ এর মধ্যে তুলনা করব , যেহেতু ১<৩৫ সেহেতু ১ এবং ৩৫ আগের অবস্থাতেই থাকবে ।  এবার ৬২ ও ১৫ এর মধ্যে তুলনা করব , এখানে ৬২ > ১৫ ,  তাই ১৫ আগে চলে আসবে এবং ৬২ পরে চলে যাবে । নিচের চিত্রে খেয়াল করুন ! 
 


 
   
 
এখন আমাদের হাতে দুইটা দুইটা করে মোট চারটা সেট রয়েছে যেখানে সবাই সর্টেড । এরা মূলত আমাদের ভাগকরা সাবসেট ! এবার বাম পাশের দুইটা সেটের প্রথম এলিমেন্টগুলোকে কম্পেয়ার করে সর্ট করব । প্রথমে ২ আর ৫ এর মধ্যে কম্পেয়ার করব , যেহেতু  ২< ৫  তাই ২ প্রথম স্থানেই থাকবে ! এবারে ৫ এর সাথে ৪৫ কে কম্পেয়ার করব । এখানে ৪৫ > ৫  , তাই ৫ চলে আসবে দ্বিতীয় স্থানে । বাকি রইল ৫১ , এবার আবার ৪৫ এর সাথে ৫১ কে তুলনা করব । ৪৫ < ৫১ তাই ৪৫ চলে আসবে তৃতীয় স্থানে এবং ৫১ চতুর্থ স্থানে ।

 
                       
   এবার বাম পাশের মতই ডান পাশের দুই সেটের প্রথম এলিমেন্ট একটার সাথে আরেকটার তুলনা করে সর্ট করব । প্রথমে ১ এবং ১৫ এর তুলনা করব । ১ < ১৫ তাই প্রথমে ১ থাকবে , এবার ১৫ এর সাথে ৩৫ এর তুলনা করব । ৩৫ > ১৫  , তাই ১৫ চলেযাবে দ্বিতীয় স্থানে । এবার ৩৫ এর সাথে ৬২ দিয়ে তুলনা করব , ৩৫ < ৬২ তাই যথারীতি ৩৫ তৃতীয় এবং ৬২ চতুর্থ স্থানে থাকবে । নিচের চিত্রে লক্ষ করুন ~



এখন আমাদের হাতে আছে দুইটা সেট , যাদের কে আমরা এতক্ষণ সর্ট করেছি । 

 
এবার আগের মতই দুই সেটের প্রথম দুইটা এলিমেন্ট একটার সাথে আরেকটার তুলনা করব , প্রথমে ২ এবং ১ এর তুলনা করব । ২> ১ তাই ১ চলে আসবে প্রথমে । এবার ২ এর সাথে ১৫ এর তুলনা করব , এখানে ২ < ১৫ তাই ২ সামনে চলে আসবে । এবার ১৫ এবং ৫ এর তুলনা করব , ১৫>৫ তাই ৫ আগে চলে আসবে । এবার ১৫ এর সাথে ৪৫ এর তুলনা করব , ১৫ <৪৫ তাই ১৫ আগে চলে আসবে ।
এবার ৪৫ এর সাথে ৩৫ এর তুলনা করব , ৪৫ > ৩৫ তাই ৩৫ আগে চলে আসবে । এবার ৪৫ এবং ৬২ এর তুলনা করব , ৪৫ < ৬২ তাই ৪৫ আগে চলে আসবে । এবার ৬২ এবং ৫১ এর তুলনা করব , ৬২ > ৫১ তাই ৫১ আগে  । এবারে ৬২র সাথে তুলনা করার মত কোন ইলিমেন্ট নেই তাই ৬২ সবার পরে চলে যাবে । নিচের চিত্রে খেয়াল করুন ~


পুরো ব্যাপারটা হচ্ছে , প্রথমে আমরা অ্যারেকে দুই ভাগে ভাগ করতে থাকব , যতক্ষণ  পর্যন্ত সিঙ্গেল এলিমেন্ট না হয় । তার পরে সর্ট করে করে নিচ থেকে উপর পর্যন্ত যাব । এটাকে রিকার্সন বলা হয় ।

আর এই পর্যন্তই , কোন প্রশ্ন থাকলে কমেন্টে অথবা মেইল করতে পারেন  !
http://facebook.com/sajibcpi

2

Science and Information / Re: এলগরিদমের খুঁটিনাটি

« on: October 08, 2017, 03:57:13 PM »

Thank you sir

3

Science and Information / এলগরিদমের খুঁটিনাটি ~ তৃতীয় পর্ব ( সর্টিং এলগরিদম ) !

« on: September 21, 2017, 01:16:18 AM »

ধরুন আপনাকে কয়েকটা অগোছালো সংখ্যা  দিলাম , আর বললাম আমাকে এই সংখ্যাগুলো ছোট থেকে বড়  আকারে সাজিয়ে দিন ! সংখ্যাগুলোকে ক্রমান্বয়ে ছোট থেকে বড় আকারে সাজানোর জন্য আপনি কি করবেন ? একটু ভাবুনতো,  কি করলে অগোছালো কয়েকটা সংখ্যাকে ক্রমান্বয়ে ছোটথেকে বড় করা যায় ! থাক এতো চিন্তা করতে হবেনা , আমিই বলে দিচ্ছি কি করে করা যায়
ধরুন ৫ ৯ ০  ৮ এই চারটা সংখ্যাকে ছোট থেকে বড় আকারে ক্রমান্বয়ে সাজালে হয় ০ ৫ ৮ ৯ । এখন যদি আপনাকে ১০ হাজারটা অগোছালো  সংখ্যাকে ছোট থেকে বড় আকারে সজিয়ে দিতে বলা হয় তখন কি করবেন ?  হ্যাঁ তখনি আপনার কম্পিউটারের সাহায্য নিতে হবে , আর এই অগোছালো সংখ্যাকে গোছানোর জন্য কম্পিউটার কয়েকটা এলগরিদম ব্যাবহার করে  । আর সে গুলোকেই বলাহয় সর্টিং এলগরিদম  ।

অগোছালো সংখ্যাকে গোছানোর জন্য বেশ কয়েকটি এলগরিদম রয়েছে ~
Bubble Sort
Insertion Sort
Selection Sort
Quicksort
Mergesort
Heapsort

আজ আলোচনা করব Bubble Sort Algorithm নিয়ে !  বলে রাখা ভালো , বর্তমানে Bubble Sort এলগরিদম ব্যাবহার করা হয়না বললেই চলে । তবে নতুনদের বুঝার জন্যই মূলত আজকের এই লেখা ।  আসুন দেরী না করে  শিখে ফেলি Bubble Sort এলগরিদম কিভাবে কাজ করে । Bubble Sort একটা সংখ্যার সাথে আরেকটা সংখ্যার তুলনা করে তাদেরকে ক্রমান্বয়ে সাজায় ।

5 1 4 2 8  এই কয়েকটা অগোছালো সংখ্যা নিলাম - এখন Bubble সর্ট এর  নিয়ম অনুযায়ী  5 এবং 1 এর মধ্যে তুলনা করব , যেহেতু 5 এর চেয়ে 1 ছোট সেহেতু 1 আগে চলে যাবে এবং 5 সামনে চলে যাবে ।
প্রথম ধাপঃ-    ( 5 1 4 2 8 ) –> ( 1 5 4 2 8 ) এখানে  5 > 1   
                    এবার 5 এর সাথে 4 এর তুলনা করব , যেহেতু 5 এর চেয়ে 4 ছোট সেহেতু 4 সরে গিয়ে 5 এর স্থানে বসে যাবে ।
                    ( 1 5 4 2 8 ) –>  ( 1 4 5 2 8 ), কারণ  5 > 4
                      এবার 5 এর সাথে 2  এর তুলনা করব
                    ( 1 4 5 2 8 ) –>  ( 1 4 2 5 8 )  এখানে  5 > 2
                    এবারে 5 এর সাথে 8 এর তুলনা করব , যেহেতু 8 আগে থেকেই বড় সেক্ষেত্রে এখানে কোন পরিবর্তন হবে না ।
                    ( 1 4 2 5 8 ) –> ( 1 4 2 5 8 )

দ্বিতীয় ধাপঃ-
( 1 4 2 5 8 ) –> ( 1 4 2 5 8 )
( 1 4 2 5 8 ) –> ( 1 2 4 5 8 ), এখানে  4 > 2
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –>  ( 1 2 4 5 8 )
এখানেই আমাদের সর্টিং শেষ , কিন্তু  আমাদের এলগরিদম এটা জানেনা ! যতক্ষণ না পর্যন্ত আর কোন সংখ্যার সোয়াপিং হয় । তাই পুরো প্রসেসটা আবার শেষ বারের মত করতে হবে !
সর্বশেষ ধাপঃ
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )

                                                                                            আসুন এবারে একটা  ভিজুয়্যালি উদাহরণ  দেখে নেই  ~
                                                   
                                                                                                       
আজ এই পর্যন্তই , সময়ের অভাবে নিয়মিত লেখা দিতে পারিনা বলে দুঃখিত । সামনের পর্বে বাকি সর্টিং এলগরিদমগুলো নিয়ে লিখব ইনশাআল্লাহ  ! ততদিন ভালো থাকুন , প্রযুক্তির সাথে থাকুন

4

Science and Information / এলগরিদমের খুঁটিনাটি ২য় পর্ব (গুগল রহস্য )

« on: August 05, 2017, 03:57:22 PM »

আগের পর্ব পড়ে থাকলে আপনি এতক্ষণে নিশ্চই জেনে গেছেন , এলগরিদম কি এবং এলগরিদমের ব্যাবহার । না পড়লেও সমস্যা নেই,   http://forum.daffodilvarsity.edu.bd/index.php/topic,44622.0.html এখান থেকে  পড়ে নিতে পারেন ।
আজ পরিচয় করিয়ে দিব টেক জায়েন্ট কোম্পনি গুগলের প্রথম দিকের  এলগরিদমের সাথে , এই এলগরিদম দিয়েই আজকের গুগলের উত্থান । 
১৯৯৬ সালে গুগল ছিল Stanford University র দুই ছাত্র Larry Page এবং  Sergey Brin এর PDH র টপিক ।
 ১৯৯৮ সালের সেপ্টেম্বরের ৪ তারিখ সার্চ ইঞ্জিন হিসেবে গুগল তার পথচলা শুরু করে ! গুগল তখনো অন্যান্য সাধারন সার্চ ইঞ্জিনের মতই ছিল ।
ততদিনে Larry Page একটা একগরিগম আবিষ্কার করেন , আর এই এলগরিদমই গুগলকে সাধারণ থেকে বানিয়ে দেয় অসাধারণ । Larry Page  এর নাম থেকেই সে এলগরিদমের নামকরন করা হয় Page Rank Algorithm .
চলুন দেখেনেয়া যাক Page Rank Algorithm রহস্য !
পেজ রেঙ্ক কি ?
একটি পেজ (Web page) ইন্টারনেটে কতটা গুরুত্ত্বপূর্ন তা নির্ধারন করে পেজ রেঙ্ক এলগরিদম ! যারা Search Engine Optimization নিয়ে কাজ করেছেন কিংবা এটা নিয়ে  সামান্য পরিমাণ ইনফরমেশন ও জানেন তাদের বুঝতে সুবিধা হবে ।
পেজ রেঙ্ক বুঝতে হলে প্রথমেই জানতে হবে Backlink সম্পর্কে , যদি একটা পেজ A থেকে একটা লিংক পেজ B এ যায় , তাহলে পেজ B এর কাছে পেজ A এর একটা ব্যাকলিংক আছে ।  তার মানে,  যে পেজের কাছে যত বেশি Backlink আছে , সে পেজ ততটা গুরুত্বপূর্ন !
Page Rank কে ভোটের সাথে তুলনা করা যেতে পারে , আর ইনকামিং লিংক গুলো হচ্ছে ভোট । সবচেয়ে বেশি ভোট (ইনকামিং লিংক ) পাওয়া পেজই হচ্ছে সবচেয়ে গুরুত্ত্বপূর্ন !
নিচের চিত্রে খেয়াল করুন –

Page A ইনকামিং লিংক ১ টা , তার মানে পেজ A এর কাছে একটা Backlink আছে ।  তেমনি Page B তে  ১ টা , Page C তে  ৩ টা , Page D তে কোন ইনকামিং লিংক নেই !
তাহলে আপনিই বলুন এখানে চারটা পেজের মধ্যে কোন পেজটা সবচেয়ে গুরুত্বপূর্ন ?
এবার এই চিত্রটা খুব ভালোভাবে লক্ষ্য করুন ~~


সমস্যাটা ধরতে পেরেছেন ? না পারলেও কোন সমস্যা নাই , এখনি পেরে যাবেন 
পেজ E এর কাছে ৬টা  ইনকামিং লিংক থাকার পরও কেন রেটিং এত কম , আবার মাত্র একটা ইনকামিং লিংক দিয়েই পেজ C  রেংকিং এ  দ্বিতীয় !
এখন প্রশ্ন করতে পারেন , ক্যামনে কি ?
হ্যাঁ এটাই Page Rank এলগরিদমের রহস্য ! ঐ যে বললাম পেজ রেঙ্ক ভোটের মত , আসলে যত বেশি গুরুত্বপূর্ন পেজ থেকে আপনি ভোট (ইনকামিং লিংক ) পাবেন ততবেশি আপনিও গুরুত্বপূর্ন ! এটাই হচ্ছে Page Rank Algorithm এর মূল তত্ত ।
আশাকরি এতক্ষণে পেজ রেঙ্ক এর সাধারণ ধারণাটা পেয়ে গেছেন , আজ এই পর্যন্তই !আগামী পর্বে Page Rank Algorithm এর গাণিতিক ব্যাখ্যা ও প্রোগ্রামিং ল্যাংগুয়েজ দিয়ে পেজ রেঙ্ক এলগরিদম করা দেখাব  ইনশাআল্লাহ্‌ ।
ততক্ষণ প্রযুক্তির সাথেই থাকুন , ধন্যবাদ  ।






 

5

Science and Information / Re: এলগরিদমের খুঁটিনাটি

« on: August 03, 2017, 12:09:29 AM »

ধন্যবাদ

6

Science and Information / এলগরিদমের খুঁটিনাটি

« on: August 01, 2017, 11:07:44 PM »

যাদের এলগরিদম নিয়ে আগ্রহ আছে কিন্তু তেমন কিছুই জানেন না , এই লেখাটি শুধুমাত্র তাদের জন্য । আসুন প্রথমেই এলগরিদমের নামকরণ সম্পর্কে কিছু তথ্য জেনে নেয়া যাক । Algorithm শব্দটি এসেছে ল্যাটিন শব্দ algorismus থেকে , নবম শতাব্দীর পার্সিয়ান গণিতবিদ Al-Khwarizmi র নাম থেকেই মূলত এলগরিদম নামকরণ করা হয় ।
এলগরিদম কি ?
কোন একটি সমস্যা সমাধানের ধারাবাহিক ধাপের সমষ্টিকেই এলগরিদম বলে । সহজ ভাষায় , কোন একটি কাজ সম্পন্ন করার সুনির্দিষ্ট ধাপগুলোর সমষ্টিই এলগরিদম !
দৈনন্দিনের কাজ থেকে শুরু করে গাণিতিক সমস্যার সমাধান , কম্পিউটার প্রোগ্রাম , রোবটিক্স , আর্টিফিসিয়াল ইন্টেলিজেন্সি সব জায়গাতেই এলগরিদমের ব্যাবহার রয়েছে ।
উদাহরণ হিসাবে তরকারী রান্নার কথাই ধরুন , বাজার থেকে তরকারী কিনে রান্না করা পর্যন্ত কয়েকটা ধাপ সম্পন্ন করলেই তরকারী রান্না করা সম্ভব ।  রান্নার এই  ধাপগুলোর উপরই তরকারির স্বাদ এবং মান নির্ভর করে । ঠিক তেমনি কোন সমস্যা সমাধানের ধাপগুলোর উপর সুন্দর এবং দ্রুত সমাধান নির্ভর করে । এই ধাপগুলোর সমষ্টিই হচ্ছে এলগরিদম ।
একই তরকারি যেমন বিভিন্ন ভাবে রান্না করা যায় , ঠিক তেমনি একটি সমস্যা অনেক রকম ভাবেই সমাধান করা যায় ।প্রত্যেকটি সমস্যার জন্য আলাদা আলাদা এলগরিদম রয়েছে , আবার  একই সমস্যা সমাধানের জন্য অনেকগুলো এলগরিদম থাকতে পারে ! সাধারণত এলগরিদমকে Pseudocode বলা হয় । 
কম্পিউটার বিজ্ঞানে এলগরিদমঃ-
কম্পিউটার বিজ্ঞান এবং এলগরিদম একই সুতোয় বাঁধা ! এক কথায় বলতে গেলে এলগরিদম ছাড়া কম্পিউটার বিজ্ঞানের কথা ভাবাই যায় না ।  আপনার স্মার্ট ফোন , কম্পিউটার , ওয়াইফাই রাউটার থেকে শুরুকরে সোশ্যাল নেটওয়ার্কিং সাইট , ই-কমার্স , সার্চ ইঞ্জিন সব কিছুই চলে এলগরিদমের উপর নির্ভর করে ।এক কথায় বলা যায় , বর্তমান প্রযুক্তি পুরোপুরি এলগরিদমের উপর নির্ভরশীল । 
উদাহরন হিসাবে গুগল ম্যাপের কথাই বলি , আমরা প্রায় সবাই গুগল ম্যাপ সম্মন্ধে জানি এবং দরকারে ব্যবহার করি । ধরুন ,  আপনি ঢাকা থেকে চট্টগ্রাম যাবেন , গুগল ম্যাপে সার্চ করলে দেখবেন কুমিল্লা হয়ে ঢাকা চট্টগ্রাম মহাসড়কের ডিরেকশন দেখাচ্ছে । কিন্তু আপনি ইচ্ছা করলে ভৈরব দিয়েও ঘুরে যেতে পারবেন , তাহলে কেন সরাসরি ঢাকা চট্টগ্রাম মহাসড়কের ডিরেকশন দেখাচ্ছে ?
কারন একটাই , সবচেয়ে কম সময় যে রাস্তায় লাগবে গুগল ম্যাপ সে রাস্তাই দেখাবে । এখানে সবচেয়ে ছোট রাস্তা বের করার জন্য Shortest path Algorithm ব্যাবহার করা হয়েছে ।
প্রতিনিয়ত কম্পিউটার বিজ্ঞানে অসংখ্য এলগরিদম ব্যাবহার করা হচ্ছে , ২য় পর্বথেকে জনপ্রিয় সব এলগরিদম নিয়ে লিখব ইনশাআল্লাহ্‌ !
আসুন পৃথিবীর বিশেষ বিশেষ কিছু এলগরিদমের সাথে পরিচিত হই ।
1.   Merge Sort, Quick Sort and Heap Sort
2.   Dijkstra’s algorithm
3.   Secure Hash Algorithm
4.   Link Analysis
5.   Fourier Transform and Fast Fourier Transform
 এই পর্বের উদ্দ্যেশই হচ্ছে নতুনদের কাছে এলগরিদমের পরিচয় করিয়ে দেয়া , পরবর্তি পর্ব থেকে স্পেসিফিক কোন এলগরিদম নিয়ে লিখব । প্রযুক্তির সাথেই থাকুন , ধন্যবাদ 